This is a fun tool I made that convolves a source image with a hex-grid dithering shader I wrote. Try loading an image, playing with the parameters and see what you come up with! All the image processing is done in a few shaders in client-side WebGL, so don't worry about me stealing your images or anything.

Explanation

Tesselation

To break down a hexagon grid to a tesselating pattern, I draw, on each hexagon on the grid, a line from every other vertex to the center.

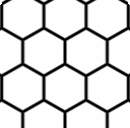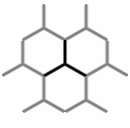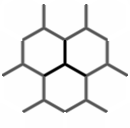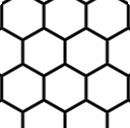
Density Transition

To transition from one density level to the next, each hexagon vertex where three lines meet expands to form a hexagon. At the same time, each line splits to two other lines, which rotate away from each other. When the transformation is complete, the resulting hexagon grid has smaller side length by a factor of √3

Steps

For a given pixel, we index to the step of density required by the input greyscale value, performing the necessary transformations to position it correctly relative to the previous step of density. The "Steps" parameter controls the number of steps through which the filter passes on its way from its lowest density to its highest density.

Blur

Since the convolution is 'continuous' (not in a strict mathematical sense), we get smooth transitions across input values. However, most source images are not necessarily smooth pixel-to-pixel. It's a stylistic choice, but applying a Gaussian blur to the image prior to convolving it with the hexagon density function gets rid of most pixelation of the source image. However, sometimes it can look better to include those artifacts, or keep the blur radius small.

Gamma

Raising the incoming greyscale value (normalized from 0 to 1) to some gamma value gives us control over whether contrast is highlighted more on dark parts or light parts of the image.

Appearance

Finally, I added controls to invert the incoming greyscale value, swap which colors are used for the lines and hexagons, and change the thickness and width of the lines. These parameters should be relatively self-explanatory as soon as you play with the sliders :)

Many thanks to Red Blob Games for their write-up on axial coordinate systems, without which this whole thing would have taken me ages to figure out. Thanks also to WebGLFundamentals for their tutorials on using WebGL. Great for anyone with experience in OpenGL like me, or really anyone interested in in-browser rendering with WebGL.